Pre-Lie algebra

In mathematics, a pre-Lie algebra is an algebraic structure on a vector space, that describes some properties of objects such as rooted trees and vector fields on affine space.

The notion of pre-Lie algebra has been introduced by Murray Gerstenhaber in his work on deformations of algebras.

Pre-Lie algebras have been considered under some other names, among which one can cite left-symmetric algebras, right-symmetric algebras or Vinberg algebras.

Definition

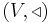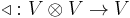A pre-Lie algebra $(V,\triangleleft)$ is a vector space $V$ with a bilinear map $\triangleleft�: V \otimes V \to V$ , satisfying the relation $(x \triangleleft y) \triangleleft z - x \triangleleft (y \triangleleft z) = (x \triangleleft z) \triangleleft y - x \triangleleft (z \triangleleft y).$

This identity can be seen as the invariance of the associator 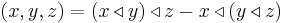$(x,y,z) = (x \triangleleft y) \triangleleft z - x \triangleleft (y \triangleleft z)$ under the exchange of the two variables $y$ and $z$ .

Every associative algebra is hence also a pre-Lie algebra, as the associator vanishes identically.

Examples

Vector fields on the affine space

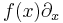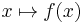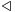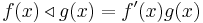If we denote by $f(x)\partial_x$ the vector field $x \mapsto f(x)$ , and if we define $\triangleleft$ as $f(x) \triangleleft g(x) = f'(x) g(x)$ , we can see that the operator 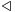$\triangleleft$ is exactly the application of the 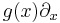$g(x)\partial_x$ field to 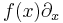$f(x)\partial_x$ field.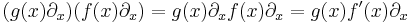 $(g(x)\partial_x)(f(x)\partial_x) = g(x) \partial_x f(x) \partial_x = g(x) f'(x) \partial_x$

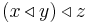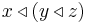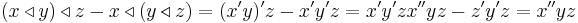If we study the difference between $(x \triangleleft y) \triangleleft z$ and $x \triangleleft (y \triangleleft z)$ , we have $(x \triangleleft y) \triangleleft z - x \triangleleft (y \triangleleft z) = (x' y)'z - x'y'z = x'y'z x''yz - z'y'z = x''yz$ which is symmetric on y and z.

Rooted trees

Let 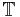$\mathbb{T}$ be the vector space spanned by all rooted trees.

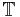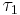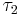One can introduce a bilinear product $\curvearrowleft$ on $\mathbb{T}$ as follows. Let $\tau_1$ and $\tau_2$ be two rooted trees.

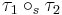$\tau_1 \curvearrowleft \tau_2 = \sum_{s \in \mathrm{Vertices}(\tau_1)} \tau_1 \circ_s \tau_2$

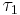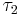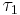where $\tau_1 \circ_s \tau_2$ is the rooted tree obtained by adding to the disjoint union of $\tau_1$ and $\tau_2$ an edge going from the vertex $s$ of $\tau_1$ to the root vertex of $\tau_2$ .

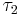Then 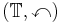$(\mathbb{T}, \curvearrowleft)$ is a free pre-Lie algebra on one generator.

References

Chapoton, F.; Livernet, M. (2001), "Pre-Lie algebra and the Rooted Trees Operad", I.M.R.N. 8: 395–408 .
Szczesny, M., Pre-Lie algebras and incidence categories of colored rooted trees .